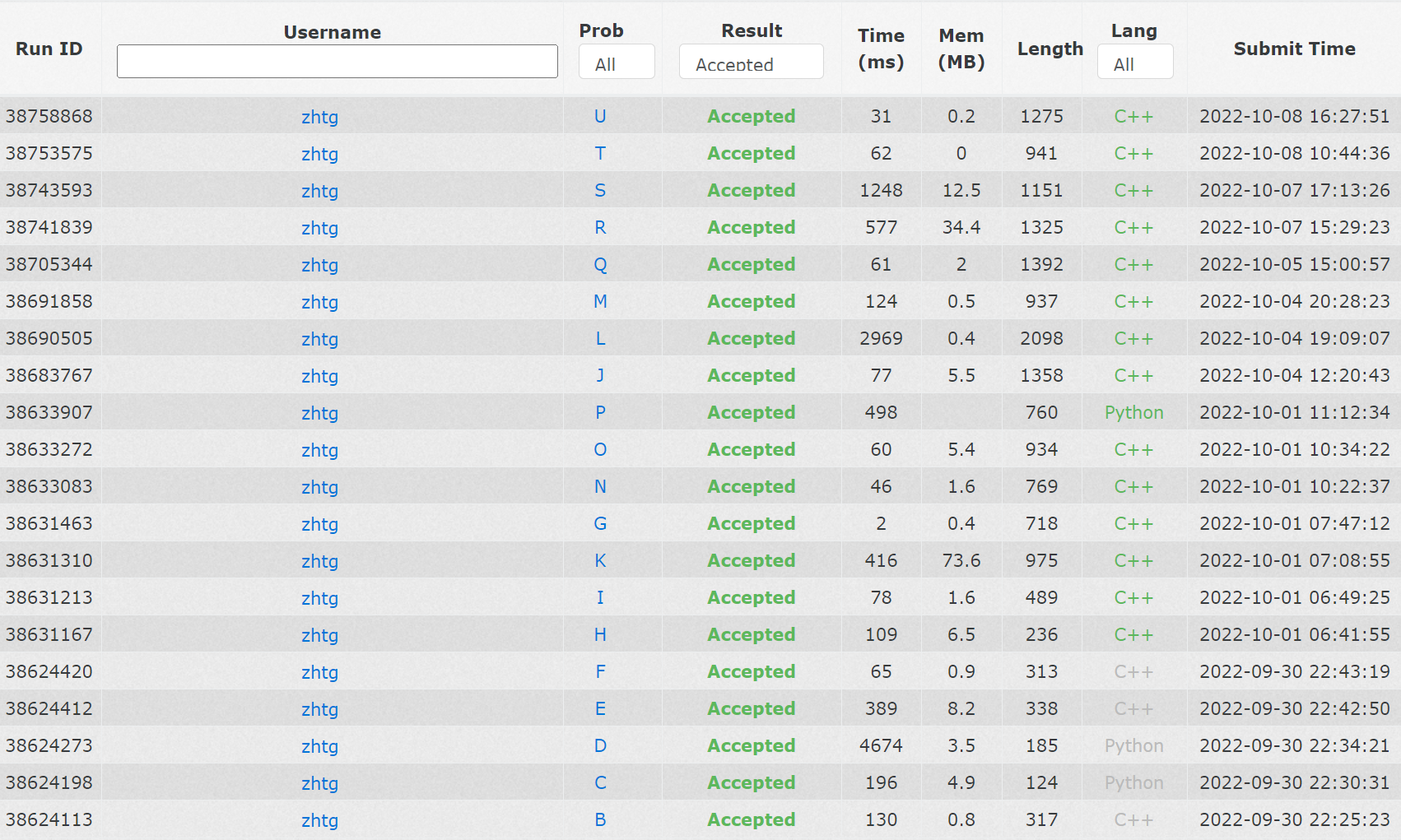
题目情况 & 练后总结
| 序号 | 名称 | 知识点 |
|---|---|---|
| A | 超级楼梯 | 递推(起点为1) |
| B | 台阶问题 | 递推(起点为0) |
| C | 数楼梯 | 递推(起点为0)、高精度 |
| D | 等差数列 | 递推、高精度 |
| E | 查找 | 二分查找 |
| F | 数的计算 | 递推 |
| G | 二项式 | 递推 |
| H | 数数 | STL的set 等方法 |
| I | 两数之和 | 二分查找 |
| J | Ehab and Path-etic MEXs | 思维题(构造答案) |
| K | Max Mod Min | 思维题、双端队列 |
| L | Matrix Power Series | 矩阵快速幂 |
| M | Hot Black Hot White | 思维题(构造答案) |
| N | Coin Rows | 思维题 |
| O | Aggressive cows | 二分 |
| P | Chat Ban | 二分、高精度 |
| Q | Binary String | 二分 |
| R | Integers Have Friends | 二分、思维题(数学小技巧) 、st表 |
| S | For Gamers. By Gamers. | 二分 |
| T | Guess the Permutation | 二分、思维题(数学小技巧) |
| U | 卷王的测试(Hemose in ICPC ?) | 二分、思维题 |
(用Python写的基本上是高精度题目偷懒QAQ……快进到迎新赛出高进度刷掉我)
只有一句感言:好多的gcd和数学小技巧!
A – 超级楼梯
递推入门题。到达该层楼可行的方案数量,为之前所有能到达 该层 的所有 前置层 的方案总和。接下来几道楼梯题思路基本相同,就是注意一下每一题的出发层是第一层还是第〇层。
#include<bits/stdc++.h>
using namespace std;
int ai[50],n,_t;
int main(){
ai[1] = 1 ;ai[2] = 1;
for(int i=3;i<=49;i++){
ai[i] = ai[i-1] + ai[i-2];
}
scanf("%d",&_t);
while(_t--){
scanf("%d",&n);
printf("%d\n",ai[n]);
}return 0;
}B – 台阶问题
#include<bits/stdc++.h>
using namespace std;
int ai[1000005],n,k;
int main(){
ai[0] = 1;
scanf("%d%d",&n,&k);
for(int i=1;i<=n;i++){
ai[i] = 0;
for(int j=i-1;j>=max(i-k,0);j--){
ai[i] = (ai[i] + ai[j]) % 100003;
}
}
printf("%d\n",ai[n]);return 0;
}C – 数楼梯
注意高精度。
ai = [0] * (10000)
ai[0] = ai[1] = 1
n = int(input())
for i in range(2,n+1):
ai[i] = ai[i-1] + ai[i-2]
print(ai[n])D – 等差数列
注意高精度。
# 请原谅我高精度模板不见了
s = input().split()
a1 = int(s[0])
a2 = int(s[1])
n = int(s[2])
ans = a1 + a2
cur = a2
for i in range(3,n+1):
cur += (a2 - a1)
ans += cur
print(ans)E – 查找
二分入门题,甚至已经给你排序好了。(你已经学会了二分算法,现在就去解决“卷王的测试”的前一题吧!(雾))
#include<bits/stdc++.h>
using namespace std;
long long ai[1000005],n,m,q,p;
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++){
scanf("%d",&ai[i]);
}
while(m--){
scanf("%d",&q);
p = lower_bound(ai+1,ai+n+1,q) - ai;
printf("%d ",(p>n||ai[p]!=q)?-1:p);
}
return 0;
}F – 数的计算
典型递推思想,每一个数字可行方案数量为所有可能情况包含的方案数之和。注意到对于相同的数,对其做“数的计算”的结果总是相同的,因此可以存值减少重复计算。感谢SATSKY在群里指出最终结果一致但是可用两种方法递推得到的话,是算两个数。
#include<bits/stdc++.h>
using namespace std;
int x,f[2000];
int count(int x){
if(f[x]){
return f[x];
}
if(x%2==0){
f[x] = count(x-1)+count(x/2);
}else{
f[x] = count(x-1);
}
return f[x];
}
int main(){
f[0]=1;f[1]=1;
//while(1){
cin>>x;
cout<<count(x)<<endl;
//}
return 0;
}G – 二项式
组合数(二项式系数)的递推求法应该在高中就学过了。实在不行就想想杨辉三角。注意输出格式。计蒜客没有错误提示。
#include<bits/stdc++.h>
using namespace std;
long long ai[100][100],n,m,q,p;
int main(){
scanf("%d",&n);
ai[1][0] = 1;ai[1][1] = 1;
for(int i=2;i<=n;i++){
ai[i][0] = ai[i][i] = 1;
for(int j=1;j<i;j++){
ai[i][j] = ai[i-1][j] + ai[i-1][j-1];
}
}
if(n==1){
printf("(a+b)^1=a^1+b^1\n");
return 0;
}
if(n==0){
printf("(a+b)^0=\n");
return 0;
}
if(n==2){
printf("(a+b)^2=a^2+2ab+b^2\n");
return 0;
}
printf("(a+b)^%d=a^%d+%llda^%db",n,n,ai[n][1],n-1);
for(int i=2;i<=n-2;i++){
printf("+%llda^%db^%d",ai[n][i],n-i,i);
}
printf("+%lldab^%d+b^%d",ai[n][1],n-1,n);
return 0;
}H – 数数
用STL简直不要太无脑,或者也可以自己写hash,或者也可以排序之后前后比较,总之方法挺多的。(有一个倒霉蛋排序被卡了,然后发现是题面的锅)
#include<bits/stdc++.h>
using namespace std;
long long n,m,q,p;
int main(){
scanf("%d",&n);
set<int> s;
while(n--){
scanf("%d",&m);
s.insert(m);
}
printf("%d\n",s.size());
return 0;
}I – 两数之和
二分查找,排序之后对于每一个数查找另一个数使得两数之和符合条件。或者set遍历?
#include<bits/stdc++.h>
using namespace std;
long long ai[200005],n,m,l,r,mid,x;
int main(){
scanf("%lld%lld",&n,&m);
for(int i=1;i<=n;i++){
scanf("%lld",&ai[i]);
}
sort(ai+1,ai+1+n);
l = 1;r = n;ai[n+1]=ai[n+2]=0x3f3f3f3f3f;
for(int i=1;i<=n;i++){
if(ai[i]>(m+1)/2)break;
x = lower_bound(ai+l,ai+r+1,m-ai[i])-ai;
if(ai[x] == m-ai[i] && x!=i){
printf("YES\n");return 0;
}
}
printf("NO\n");
return 0;
}J – Ehab and Path-etic MEXs
思维题,对于“至少有一个三条出边的点”的树来说,任意路径上所有边权的最小值一定是“${0,1,2}$”中的一个,只要“$0,1,2$”分别是同一个点的三条边“$\left( u,v_1 \right) , \left( u,v_2 \right) , \left( u,v_3 \right) $”的边权。证明也很简单,因为$\left( u,v_1 \right) , \left( u,v_2 \right) , \left( u,v_3 \right) $是同一个点引出的三条边,所以对于树上的任意一条路径,最多只能经过其中的两条边。只要确保了这一点,剩下的边就闭着眼睛瞎填即可,因为任何不包含边权为$0$的路径,未出现的最小数字永远是$0$。
注意存在一种特殊情况,那就是链。对于链而言,由于没有选择的余地,所以随意构造边权即可。
#include<bits/stdc++.h>
using namespace std;
int head[100005],nxt[200010],to[200010],acnt=-1;
int inc[100005],val[200010],cnt=1,n,ai,bi,ci=-1;
pair<pair<int,int>,int> edges[100005];
inline void addEdge(int a,int b,int c){
nxt[++cnt] = head[a];
to[cnt] = b;
val[cnt] = c;
head[a] = cnt;
nxt[++cnt] = head[b];
to[cnt] = a;
val[cnt] = c;
head[b] = cnt;
edges[c] = make_pair(make_pair(a,b),0);
}
inline void dfs(int cur,int fa){
for(int i=head[cur];i!=-1;i=nxt[i]){
if(to[i] == fa)continue;
edges[val[i]] = make_pair(edges[val[i]].first,++acnt);
}
for(int i=head[cur];i!=-1;i=nxt[i]){
if(to[i] == fa)continue;
dfs(to[i],cur);
}
}
int main(){
memset(head,-1,sizeof(head));
memset(nxt,-1,sizeof(nxt));
memset(inc,0,sizeof(inc));
memset(val,0,sizeof(inc));
scanf("%d",&n);
for(int i=1;i<n;i++){
scanf("%d%d",&ai,&bi);
addEdge(ai,bi,i);
inc[ai]++;inc[bi]++;
if(inc[ai]==3){
ci = ai;
}
if(inc[bi]==3){
ci = bi;
}
}
if(ci==-1){
for(int i=0;i<n-1;i++)printf("%d\n",i);
}else{
dfs(ci,-1);
for(int i=1;i<n;i++){
printf("%d\n",edges[i].second);
}
}
return 0;
}K – Max Mod Min
ATCoder提供了一种正经的思维方案,排序后使用双端队列,但是英文苦手只能嘤嘤,看不懂证明。自己选择用堆暴力模拟,然后发现本质上也是一个双端队列……或许是殊途同归?
#include<bits/stdc++.h>
using namespace std;
long long ai[200005],n,m,l,r,mid,x,cnt;
priority_queue<pair<long long,int> > qmax,qmin;
pair<long long,int> maxp,minp;
int main(){
scanf("%lld",&n);cnt=0;
for(int i=1;i<=n;i++){
scanf("%lld",&ai[i]);
qmax.push(make_pair(ai[i],i));
qmin.push(make_pair(-ai[i],i));
}
while(!qmax.empty()){
maxp = qmax.top();qmax.pop();
if(ai[maxp.second]!=maxp.first)continue;
minp = qmin.top();
while(ai[minp.second]!=-minp.first){
qmin.pop();minp = qmin.top();
}
if(minp.second == maxp.second)break;
ai[maxp.second] = maxp.first % minp.first;
if(ai[maxp.second]!=0){
qmax.push(make_pair(ai[maxp.second],maxp.second));
qmin.push(make_pair(-ai[maxp.second],maxp.second));
}
cnt++;
}
printf("%lld\n",cnt);
return 0;
}L – Matrix Power Series
矩阵快速幂,可以用在许多意想不到的地方,比如说下面这题:
以下简要复习一下矩阵快速幂。由于学的快速幂没有出现$\left(2n\times 2n \right)$的矩阵,可能效率会不如带$\left(2n\times 2n \right)$矩阵的解决方案。
矩阵加法和矩阵乘法与正常矩阵一致,重点是矩阵乘幂和求得最终结果。
矩阵的求幂使用的是不用递归二分的分解法,将总幂数$n = i_0\times 2^0 + i_1\times 2^1 + … + i_m \times 2^m$($i_j$表示$n$的对于二进制位,$m$即二进制位数),这样设置一个$base$不断与自己相乘,再适时与$ans$进行相加操作,省去了二分带来的额外空间复杂度。注意一个矩阵的$0$次方为单位矩阵(主对角线为$1$其它为$0$)。
最终结果求解则用到了二分处理的手法。注意到对于偶数次幂来说,有这样的关系:
$$
\sum(A^n) = A^1 + … + A^\frac{n}{2} + A^1 \times A^\frac{n}{2} … + A^\frac{n}{2} \times A^\frac{n}{2} \ = (1 + A^\frac{n}{2}) \times \sum(A^\frac{n}{2})
$$
这样就为二分解决最终求和提供了思路。奇数其实也可以如法炮制:
$$
\sum(A^n) = (1 + A^\frac{n+1}{2}) \times \sum(A^\frac{n-1}{2}) + A^\frac{n+1}{2}
$$
我的这个程序写的并不好,甚至出现了玄学现象(因为用了Vector以至于在TLE的边缘疯狂试探),请大家自行找个(或者写个?)好一点的程序模板。
#include<iostream>
#include<vector>
#include<cstdio>
using namespace std;
#define MATRIX vector<vector<int> >
int n,m,k;MATRIX inited;
void print(MATRIX a){
for(int i=0;i<n;i++){
for(int j=0;j<n;j++){
printf("%d ",a[i][j]);
}
printf("\n");
}
}
MATRIX build(){
MATRIX res;vector<int> resr(n);
for(int i=1;i<=n;i++){
res.push_back(resr);
for(int j=1;j<=n;j++) res[i-1][j-1] = 0;
}
return res;
}
MATRIX build1(){
MATRIX res;vector<int> resr(n);
for(int i=1;i<=n;i++){
res.push_back(resr);
for(int j=1;j<=n;j++) res[i-1][j-1] = 0;
res[i-1][i-1] = 1;
}
return res;
}
MATRIX mul(MATRIX a,MATRIX b){
MATRIX res=build();
for(int i=0;i<n;i++){ // 选定乘行
for(int j=0;j<n;j++){ // 选定乘列
for(int k=0;k<n;k++){ // 选定被乘行
res[i][j] += a[i][k] * b[k][j];
res[i][j] %= m;
}
}
}
return res;
}
MATRIX add(MATRIX a,MATRIX b){
MATRIX res=a;
for(int i=0;i<n;i++){ // 选定乘行
for(int j=0;j<n;j++){ // 选定乘列
res[i][j] += b[i][j];
res[i][j] %= m;
}
}
return res;
}
MATRIX mypow(int kk){
MATRIX base=inited,ans=build1();
while(kk){
if(kk&1) ans = mul(ans,base);
base = mul(base,base);
kk >>= 1;
}
return ans;
}
MATRIX sum(int kk){
if(kk==1) return inited;
MATRIX ans = sum(kk/2), tmp;
if(kk%2){
tmp = mypow(kk/2+1);
ans = add(ans,mul(tmp,ans));
ans = add(ans,tmp);
}else{
tmp = mypow(kk/2);
ans = add(ans,mul(ans,tmp));
}
return ans;
}
void input(){
inited = build();
for(int i=0;i<n;i++){
for(int j=0;j<n;j++){
scanf("%d",&inited[i][j]);
}
}
}
int main(){
scanf("%d%d%d",&n,&k,&m);
input();
print(sum(k));
return 0;
}
//开始玄学M – Hot Black Hot White
思维题,由于三的特性(对该数求3余等于对该数所有数位求和然后求3余),拼接两数只是个障眼法,直接把这两数对三求余之后加起来效果和老实去拼接数字一样。然后原式就变成了:
$$
(A_i + A_j)^2 + A_i \cdot A_j \equiv Z\space mod\space 3
$$
也就是说:
$$
A_i^2 + A_j^2 + 3 \cdot A_i \cdot A_j \equiv Z\space mod\space 3
$$
然后事情就变成了求$A_i^2 + A_j^2$对三求余的结果了。由于$2^2\space Mod \space 3 = 1$,所以下表中的$1’$代表$2^2$:
| $0$ | $1$ | $1’$ | |
|---|---|---|---|
| $0$ | $0$ | $1$ | $1$ |
| $1$ | $1$ | $2$ | $2$ |
| $1’$ | $1$ | $2$ | $2$ |
最后事情就变成了构造一个答案,使得每一组里面的数字尽可能都是相同的(就是抽多补少),然后根据情况选一个$Z$。
#include<bits/stdc++.h>
using namespace std;
int n,ai[100005],cnt[3]={0,0,0},a1,cnts,maxi=0;
bool colors[100005];
int main(){
scanf("%d",&n);
memset(colors,0,sizeof(colors));
for(int i=1;i<=n;i++){
scanf("%d",&ai[i]);
ai[i] %= 3;
ai[i] = (ai[i]*ai[i])%3;
cnt[ai[i]] ++;
}
a1 = cnt[0]>cnt[1] ? 0 : 1;
printf("%d\n",(a1==0?2:0));
cnts = 0;
for(int i=1;i<=n;i++){
if(ai[i]==a1){
printf("%d",cnts>=n/2?0:1);
cnts++;
}else{
printf("0");
}
}
printf("\n");return 0;
}
//还是落后大佬太多N – Coin Rows
注意只有两列,先手吃掉了硬币之后,后手的为了分数最大化一定会想办法多吃硬币,然而因为只能单向换行一次,换行方向与先手者相同,所以只能选择其中的一列的残羹吃。(注意这组样例,如果想吃这个3就吃不到另一个7了,因为只能换一次向)
事情就变成了:选择一种切割方法,使得两块(如果只有一块了另一块明显是0)残羹的最大值最小。由于这题数据小,直接求完前缀和之后一个个枚举过来都来得及。
#include<bits/stdc++.h>
using namespace std;
namespace lovelive{
int ai[2][100005],sum[2][100005];
int n,ans=0x3f3f3f3f;
void main(){
scanf("%d",&n);
sum[0][0] = sum[1][0] = 0;ans=0x3f3f3f3f;
for(int _t=0;_t<=1;_t++){
for(int i=1;i<=n;i++){
scanf("%d",&ai[_t][i]);
sum[_t][i] = sum[_t][i-1] + ai[_t][i];
}
sum[_t][n+1] = sum[_t][n];
}
for(int i=1;i<=n;i++){
ans = min(ans,max(sum[1][i-1],sum[0][n]-sum[0][i]));
//ans = min(ans,max(sum[1][i-1],sum[0][n]-sum[0][i+1]));
}
printf("%d\n",ans);
}
}
int main(){
int _t;
scanf("%d",&_t);
while(_t--){
lovelive::main();
}
return 0;
}O – Aggressive cows
还是那句话,二分答案(也就是两头牛之间的距离),选中第一个牛棚,然后按照至少相隔x距离放牛,判断能不能放下这么多头牛。
不过代码倒是重新写了一遍。
#include<bits/stdc++.h>
using namespace std;
namespace lovelive{
int ai[100005],n,c,l,r,mid;
bool check(int preans){
int ll = 1,rr = 1,cnt = 1;
while(ll<=n){
while(rr <= n && ai[rr]-ai[ll]<preans)rr++;
if(rr > n) return false;
cnt += 1;
if(cnt>=c)return true;
ll = rr;
}return cnt>=c;
}
void main(){
scanf("%d%d",&n,&c);
for (int i = 1; i <= n; i++){
scanf("%d",&ai[i]);
}
sort(ai+1,ai+n+1);
l = 1;r = ai[n];
while(l<r){
mid = (l + r + 1) >> 1;
if(check(mid)){
l = mid;
}else{
r = mid - 1;
}
}
printf("%d\n",l);
}
}
int main(){
int _t;
scanf("%d",&_t);
while(_t--){
lovelive::main();
}
return 0;
}P – Chat Ban
二分答案(能输出的最大行数)。注意高精度
# 请原谅我高精度模板不见了
def check(preans):
global k,x
if(preans > k):
preemo = (1+k)*k//2
kk = preans - k
if(preemo + (2*k - kk - 1) * kk // 2 >= x):
return preemo + (2*k - kk) * (kk-1) // 2 < x
else:
if((1+preans)*preans//2 >= x):
return (preans-1)*preans//2 < x
return True
__t = int(input())
while(__t):
__t -= 1
s = input().split()
k = int(s[0])
x = int(s[1])
l = 1
r = 2 * k - 1
while(l<r):
mid = (l+r+1)//2
if(check(mid)):
l = mid
else:
r = mid - 1
print(l)
Q – Binary String
二分答案(可以保留的最多数量的0),然后用前缀和求0和1的数量(预先存好了每个0的位置以方便尽可能少的删除1),被删除的1的数量不大于保留的0的数量就算成功。
/////////////////////////////////
// Codeforces (不知道为什么套了个比赛用模板,然而连快读都没有)
// Powered by LoveLive Tokimeki Energy
/////////////////////////////////
#include<bits/stdc++.h>
using namespace std;
namespace lovelive{
string s;
int cnti[200005],n,zeros[200005],cnt,ll,rr;
bool check(int len){
if(!len){
for(int i=1;i<=cnt;i++){
if(cnti[zeros[i]-1]&&(cnti[n+1]-cnti[zeros[i]]))return false;
}
return true;
}
for(int i=1;i<=cnt-len+1;i++){
int l=zeros[i-1]+1,r=zeros[i+len]-1;
if((l==0?0:cnti[l-1])+(cnti[n+1]-cnti[r])<=len)return true;
}
return false;
}
void main(){
cnti[0]=0;cnt = 0;
cin>>s;n=s.size();
for(int i=1;i<=n;i++){
if(s[i-1]=='0'){
zeros[++cnt] = i;
}
cnti[i]=cnti[i-1] + s[i-1] - '0';
}
cnti[n+1]=cnti[n];
zeros[0] = -1;
zeros[cnt+1] = n+1;
ll = 0;rr = cnt;
while(ll<rr){
int mid = (ll+rr)>>1;
if(check(mid)){
rr = mid;
}else{
ll = mid + 1;
}
}
printf("%d\n",ll);
return;
}
}
int main(){
int _t;
scanf("%d",&_t);
while(_t--){
lovelive::main();
}
return 0;
}R – Integers Have Friends
数学思维题,注意到在相邻两数相减之后,那个所谓的余数$m$就在相减的过程中消去了。根据gcd的传递性,两个区间相并时的区间gcd为相并之前两个区间的gcd求gcd。由于涉及到了区间查询,需要使用相应的数据结构,因为不涉及到修改,st表线段树等均可。这里用了st表。
#include<bits/stdc++.h>
using namespace std;
namespace lovelive{
typedef long long LL;
int n,l,r,mid,ans,tmp;
LL ai[200005],bi[200005];
LL st[20][200005];
LL gcd(LL a,LL b){
LL c;if(a<b)c = a,a = b,b = c;
while(b){
c = a % b;
a = b;b = c;
}
return a;
}
LL query(int i,int j){
int k = log2(j-i+1);
return gcd(st[k][i],st[k][j-(1<<k)+1]);
}
void main(){
scanf("%d",&n);
ai[0] = 0;ans= 0;
for(int i=1;i<=n;i++){
scanf("%lld",&ai[i]);
bi[i-1] = abs(ai[i-1]-ai[i]);
st[0][i-1] = bi[i-1];
}
if(n==1){
printf("1\n");
return;
}
for(int j=1;(1<<j)<n;j++){
for(int i=1;i<n-(1<<j)+1;i++){
st[j][i] = gcd(st[j-1][i] , st[j-1][i+(1<<(j-1))]);
}
}
for(int i=1;i<n;i++){
l = i ; r = n-1;
while(l<r){
mid = (l + r + 1)>>1;
if(query(i,mid)==1) r = mid - 1;
else l = mid;
}
if(bi[i]!=1)ans = max(ans,l-i+1);
}
printf("%d\n",ans+1);
}
}
int main(){
int _t;
scanf("%d",&_t);
while(_t--){
lovelive::main();
}
return 0;
}S – For Gamers. By Gamers.
真是功亏一篑。题目中的获胜条件是这样的(小队全体在怪兽打败其中一个人之前解决怪兽,并且伤害是连续造成的,而不是按秒结算):
$$
\frac{H_j}{n\cdot d_i} < \frac{h_i}{D_j}
$$
动动手啊动动脑,移动一下项就会变成:
$$
n\cdot d_i \cdot h_i > D_j \cdot H_j
$$
这样就成功地创造了条件,可以把士兵和怪兽的数值分开处理。然后,由于在每一场战斗开始之前,都会进行初始化(没有士兵,并且总是有$C$的预算),所以之前的操作使得预处理只需要进行一次,即可一招鲜吃遍所有怪兽。但是题目中还有一个“花费”的设定,如果可行,我们需要在花费最低的情况下解决怪兽。
注意到总预算的数据范围允许开数组储存,以至于预处理和二分的核心都落到了Cost上。在预处理的时候,可以储存使用一定花费所能取到的最大战力值($n\cdot d_i \cdot h_i$),这样在二分的时候可以直接二分答案并根据预处理的最大战力值判断使用这么多预算是否可行。
预处理的优化又是一大关键。光是按照每个士兵的战力值处理并不够,这样全是$1\times 1$的微型军团可以直接卡TLE。注意到对于战力值相同(或者后者更少)的两个士兵而言,若后者的花费更多,那么它相对于前者一定不是最优,可以直接以单调队列精神continue掉。
#include<bits/stdc++.h>
using namespace std;
long long cost[1000005];
pair<long long,long long> warrs[300005];
long long n,m,d,h,c,cc,l,r,minc=0x3f3f3f3f3f,mid;
int main(){
scanf("%lld%lld",&n,&cc);
for(int i=1;i<=n;i++){
scanf("%lld%lld%lld",&c,&d,&h);
warrs[i] = make_pair(-d*h,c);
}
sort(warrs+1,warrs+1+n);
memset(cost,0,sizeof(cost));
for(int i=1;i<=n;i++){
if(warrs[i].second >= minc)continue;
//使用单调队列思想优化
minc = warrs[i].second;
for(int j=1;j*minc<=cc;j++){
cost[j*minc] = max(cost[j*minc],-warrs[i].first*j);
}
}
for(int i=1;i<=cc;i++){//注意可能存在预算花不完有剩余的情况
cost[i] = max(cost[i-1],cost[i]);
}
scanf("%lld",&m);
while(m--){
scanf("%lld%lld",&d,&h);
l = 1;r = cc;minc = d * h;
while(l<r){
mid = (l+r)>>1;
if(cost[mid] > minc){
r = mid;
}else{
l = mid + 1;
}
}
printf("%lld\n",cost[l] > minc?l:-1);
}
return 0;
}T – Guess the Permutation
打codeforces经常交互题暴毙,为了求稳于是全部用了cin/cout,因为在没有加所谓的优化手段的时候,endl是有flush的效力的,不用刻意加所谓的flush函数。
注意到原数组在进行两次翻转之后出现了两个完全逆序的子数组。对于完全逆序的长度为$n$子数组,若删去开头变成长度为$n-1$的逆序子数组,逆序对正好减少了$n-1$个!了解了这一点,求全逆序对的长度就变得轻而易举,对于每一组逆序子数组只需要两次查询(包含和删去开头)即可求得长度,求长度的查询仅进行了四次。
剩下的就是寻找逆序子数组的开头了。注意到顺序子数组的逆序对数量为0,利用这点进行二分即可。
#include<bits/stdc++.h>
using namespace std;
namespace lovelive{
typedef long long LL;
LL i,j,k,n,l,r,mid,tmp;
inline long long query(LL a,LL b){
cout<<"? "<<a<<" "<<b<<endl;cout.flush();
LL ans;cin>>ans;
return ans;
}
void main(){
cin>>n;
l = 1; r = n;
while(l<r){
mid = (l + r + 1)>>1;
tmp = query(l,mid);
if(tmp>0){
r = mid - 1;
}else{
l = mid;
}
}
i = l;
mid = query(i,n);
tmp = query(i+1,n);
j = min(i + mid - tmp + 1,n);
mid = query(j,n);
tmp = query(j+1,n);
k = min(j + mid - tmp,n);
//cout<<"WRONG ANSWER!!!"<<endl;
cout<<"! "<<i<<" "<<j<<" "<<k<<endl;cout.flush();
return;
}
}
int main(){
int _t;
scanf("%d",&_t);
while(_t--){
lovelive::main();
}
return 0;
}U – 卷王的测试(Hemose in ICPC ?)
一看题目:卷王的测试?!
再看Rank:已经有大佬捡走一血了?!
然后就去瞄了题解,结果马上就后悔没有多花一点时间自己想了:原来只是二分树吗?!只要点集处于同一个联通块里,那么返回的查询值一定是其中的某条边的权值,毕竟经过两条边再做gcd结果一定不会大于两条边中任意一条边的权值。
最后就只剩下如何处理以让每次选择的点集s总是处于同一个联通块里。这里选择现场复习(也许是现学新知识?)树的欧拉序,在欧拉序的一个连续区间内的所有点正好具有这个性质。
#include<bits/stdc++.h>
using namespace std;
int head[2005],nxt[5005],to[5005],vcnt=0;
int olah[5005],olahcnt=0,maxgcd=0,a,b,n,c;
int query(int l,int r){
set<int> flag;
cout<<"? ";
for(int i=l;i<=r;i++){
flag.insert(olah[i]);
}
cout<<flag.size()<<" ";
for(set<int>::iterator i=flag.begin();i!=flag.end();i++){
cout<<(*i)<<" ";
}
cout<<endl;int tmp; cin>>tmp;
return tmp;
}
bool check(int l,int r){
int tmp=query(l,r);
return tmp==maxgcd;
}
void dfs(int cur,int fa){
olah[++olahcnt] = cur;
for(int i=head[cur];i!=-1;i=nxt[i]){
if(to[i]==fa) continue;
dfs(to[i],cur);olah[++olahcnt]=cur;
}
}
void __addEdge(int u,int v){
nxt[++vcnt] = head[u];
to[vcnt] = v;
head[u] = vcnt;
}
void addEdges(int u,int v){
__addEdge(u,v);__addEdge(v,u);
}
int main(){
cin>>n;
memset(head,-1,sizeof(head));
memset(nxt,-1,sizeof(nxt));
for(int i=1;i<n;i++){
cin>>a>>b;addEdges(a,b);
}
dfs(1,0);
cout<<"? "<<n<<" ";
for(int i=1;i<=n;i++)cout<<i<<" ";
cout<<endl;cin>>maxgcd;
a=1;b=olahcnt;
while(a+1<b){
c = (a+b) >> 1;
if(check(a,c))b = c;
else a = c;
}
cout<<"! "<<olah[a]<<" "<<olah[b]<<endl;
return 0;
}